Hier is een algebraïsche benadering om de randtoestand te begrijpen. Laten we beginnen met een generieke Dirac Hamiltoniaan voor de bulkfermionen in de $ d $ -dimensionale ruimte. $$ H = \ sum_ {i = 1: d} \ mathrm {i} \ partiële_i \ alpha ^ i + m (x_i) \ beta, $$ waarbij $ \ alpha ^ i $ en $ \ beta $ gamma-matrices tegen woon-werkverkeer zijn ($ \ {\ alpha ^ i, \ alpha ^ j \} = 2 \ delta ^ {ij} $, $ \ {\ alpha ^ i, \ beta \} = 0 $, $ \ beta \ beta = 1 $) en $ m (x_i) $ is de topologische massa die varieert in de ruimte. De grens van een topologische isolator zou overeenkomen met een knooppuntinterface waar $ m (x_i) $ van positief naar negatief gaat (of vice versa). Laten we eens kijken naar een gladde grens waarbij $ m $ verandert in de richting van $ x_1 $, wat betekent dat $ m \ propto x_1 $ in de buurt van de grens komt.

We kunnen ons dus concentreren in de richting van $ x_1 $ en de volgende 1D effectieve Hamiltoniaan $$ H_ \ text {1D} = \ mathrm {i} \ partiële_1 \ alpha ^ 1 + x_1 \ beta bestuderen. $$ Het bestaan ​​van de grensmodus in $ H $ zou overeenkomen met het bestaan ​​van de nulmodus rond $ x_1 = 0 $ in $ H_ \ text {1D} $.

Om verder te gaan, definiëren we een annihilatieoperator $$ a = \ frac {1} {\ sqrt {2}} (x_1 + \ eta \ partiële_1), $$ met $ \ eta \ equiv \ mathrm {i} \ beta \ alpha ^ 1 $, wat analoog is naar de bekende annihilatie-operator $ a = (x + \ partiële_x) / \ sqrt {2} $ van de harmonische oscillator. De matrix $ \ eta $ heeft de volgende eigenschappen: (i) $ \ eta ^ {\ dagger} = \ eta $ en (ii) $ \ eta \ eta = 1 $, die kunnen worden afgeleid uit de algebra van $ \ alpha ^ 1 $ en $ \ beta $. De aanmaakoperator is dan $ a ^ \ dagger = (x_1- \ eta \ partiële_1) / \ sqrt {2} $, en men kan aantonen dat $$ [a, a ^ \ dagger] = \ eta. $$ Verder Meer nog, de Hamiltoniaan in het kwadraat kan worden geschreven als $$ H_ \ text {1D} ^ 2 = 2 a ^ \ dagger a, $$ waarvan de eigentoestanden hetzelfde zijn als $ H_ \ text {1D} $, met de eigenwaarden in het kwadraat. Dus een nulmodus in $ H_ \ text {1D} $ zou ook overeenkomen met een nulmodus in $ H_ \ text {1D} ^ 2 $. Omdat het spectrum van $ H_ \ text {1D} ^ 2 $ positief bepaald is, is de nulmodus ook de grondtoestand.

Van $ \ eta \ eta = 1 $ weten we dat de eigenwaarden van $ \ eta $ alleen $ \ pm1 $ kunnen zijn. Vervolgens halen we in de $ \ eta = + 1 $ deelruimte de bekende commutatierelatie op van bosonoperatoren $ [a, a ^ \ dagger] = + 1 $ (merk op dat $ a $ pendelen met $ \ eta $, geen staat uit de $ \ eta = + 1 $ subruimte). Dan wordt het duidelijk dat $ H_ \ text {1D} ^ 2 = 2a ^ \ dagger a $ gewoon het boson-getal telt (met een factor 2). Dus de nulmodus van $ H_ \ text {1D} ^ 2 $ bestaat en is slechts de bosonvacuümtoestand, gedefinieerd door $ a | 0 \ rangle = 0 $ in de $ \ eta = + 1 $ -deelruimte. De ruimtelijke golffunctie van $ | 0 \ rangle $ zal gewoon hetzelfde zijn als de grondtoestand van een harmonische oscillator, wat een Gaussisch golfpakket is $ \ exp (-x_1 ^ 2/2) $ exponentieel gelokaliseerd op $ x_1 = 0 $. In de $ \ eta = -1 $ deelruimte wordt de commutatierelatie echter omgekeerd $ [a, a ^ \ dagger] = - 1 $, wat betekent dat men de annihilatieoperator kan herdefiniëren naar $ b = a ^ \ dagger $ (met $ [b, b ^ \ dagger] = + 1 $ nu), zodat het spectrum van de Hamiltoniaan $ H_ \ text {1D} ^ 2 = 2bb ^ \ dagger = 2b ^ \ dagger b + 2 $ nu wordt begrensd door 2 van onderaf en heeft geen nulstand. Daarom hebben we door verbinding te maken met de harmonische oscillator aangetoond dat

1. de nulmodus van $ H_ \ text {1D} $ bestaat,

2. zijn interne (smaak) golfvector wordt gegeven door de eigenvectoren van $ \ eta = + 1 $,

3. zijn ruimtelijke golffunctie is exponentieel gelokaliseerd rond $ x_1 = 0 $.

Met deze resultaten kunnen we de effectieve Hamiltoniaan verkrijgen door de bulk Hamiltoniaan $ H $ te projecteren op de Hilbertruimte van de grensmodus, wat de eigenruimte is van $ \ eta = + 1 $. Dus we definiëren de projectie-operator $ \ mathcal {P} _1 = (1+ \ eta) / 2 \ equiv (1+ \ mathrm {i} \ beta \ alpha ^ 1) / 2 $, en passen die toe op de bulk Hamiltoniaan $ H \ tot H _ {\ partiële} = \ mathcal {P} _1 H \ mathcal {P} _1 $. Volgens de anti-pendeleigenschap van de gamma-matrices kunnen $ \ alpha ^ 1 $ en $ \ beta $ de projectie niet overleven, en de rest van de matrices $ \ alpha ^ i $ ($ i = 2: d $) alle pendelen door de projectie $ \ mathcal {P} $, en dus aanhouden tot de grens Hamiltoniaan $$ H_ \ partiële = \ sum_ {i = 2: d} \ mathrm {i} \ partiële_i \ tilde {\ alpha} ^ i, $ $ die de gapless edge-modi op de grens beschrijft. $ \ tilde {\ alpha} ^ i $ geeft de beperking van de matrix $ \ alpha ^ i $ aan tot de $ \ mathrm {i} \ beta \ alpha ^ 1 = + 1 $ deelruimte (de projectie zal de helft van de Hilbertruimtedimensie zijn ). Daarom kunnen we door de projectie-operator $ \ mathcal {P} _i = (1+ \ mathrm {i} \ beta \ alpha ^ i) / 2 $ de Dirac Hamiltoniaan naar de massadomeinmuur duwen loodrecht op een willekeurige $ x_i $ - richting, en verkregen de effectieve Hamiltoniaan.

Deze benadering kan ook worden toegepast om de effectieve Hamiltoniaan in de topologische massadefecten te berekenen. Beginnend met de bulk zal Hamiltoniaan meerdere topologische massa termen $ m_j $, $$ H = \ sum_ {i = 1: d} \ mathrm {i} \ partiële_i \ alpha ^ i + \ sum_ {j} m_j \ beta ^ j, $ $ waar $ m_j $ een vectorveld is in de ruimte met topologische defecten (zoals monopolen, vortexlijnen, domeinwanden etc.). We kunnen de dimensiereductieprocedure gebruiken om de dimensie van het probleem elke keer met één te elimineren, totdat we de gewenste dimensie hebben bereikt. Bij elke stap vervormen we eerst het topologische defect (door het te schalen) tot zijn anisotrope limiet, en behandelen we het probleem langs de anisotropie-dimensie als een 1D-probleem. Door de projectie-operator te gebruiken zoals hierboven beschreven, kunnen we de Hamiltoniaan projecteren op de overige dimensies, en zo de probleemdimensie met één verkleinen.

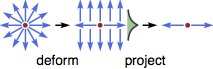
Bijvoorbeeld, als de massaveld schalen met de coördinaat als $ m_1 \ propto x_1 $, $ m_2 \ propto x_2 $, ..., dan moet de projectie-operator (tot een normalisatiefactor) $ \ mathcal {P} \ propto (1+ \ mathrm {i} \ beta ^ 1 \ alpha ^ 1) (1+ \ mathrm {i} \ beta ^ 2 \ alpha ^ 2) \ cdots $. De lage-energetische fermionmodi in het topologische defect worden gegeven door die eigentoestanden van $ \ mathcal {P} $ met eigenwaarden die niet nul zijn.

Deze benadering kan verder worden toegepast om de effectieve Hamiltoniaan in de meter defecten, zoals meterfluxen en meter monopolen. Laten we beginnen door te overwegen een flux $ \ phi $ in een 2D topologische isolator te rijgen, wat neerkomt op het graven van een rond gat en het plaatsen van de flux in het gat.

Het is handig om over te schakelen naar de poolcoördinaat en de bulk Hamiltoniaan te herschrijven als $$ H = \ mathrm {i} \ partiële_r \ alpha ^ r + \ frac {1} {r} (\ mathrm { i} \ gedeeltelijke_ \ theta-A_ \ theta) \ alpha ^ \ theta + m \ beta, $$ waar de $ (\ alpha ^ r, \ alpha ^ \ theta) $ worden geroteerd van $ (\ alpha ^ 1, \ alpha ^ 2) $ door $$ \ left [\ begin {matrix} \ alpha ^ r \\\ alpha ^ \ theta \ end {matrix} \ right] = \ left [\ begin {matrix} \ cos \ theta& \ sin \ theta \\ - \ sin \ theta& \ cos \ theta \ end {matrix} \ right] \ left [\ begin {matrix} \ alpha ^ 1 \\\ alpha ^ 2 \ end {matrix} \ right]. $ A_ \ theta $ geeft de meterverbinding aan die tot aan de flux $ \ int_0 ^ {2 \ pi} A_ \ theta \ mathrm {d} \ theta = \ phi $ door het gat integreert. Om het fermion-spectrum rond het gat te verkrijgen, moeten we de bulk Hamiltoniaan naar de cirkelvormige grens duwen door de projectie $ \ mathcal {P} = (1+ \ mathrm {i} \ beta \ alpha ^ r) / 2 $ (die is $ \ theta $ afhankelijk). Alleen $ \ alpha ^ \ theta $ zal de projectie overleven en worden beperkt tot $ \ tilde {\ alpha} ^ \ theta $ in de $ \ mathrm {i} \ beta \ alpha ^ r = + 1 $ deelruimte. Dus de energiezuinige effectieve Hamiltoniaan rond de flux is (aangenomen dat de straal van het gat $ r = 1 $ is) $$ H_ \ phi = (\ mathrm {i} \ gedeeltelijke_ \ theta-A_ \ theta) \ tilde {\ alpha} ^ \ theta = \ Big (n + \ frac {1} {2} - \ frac {\ phi} {2 \ pi} \ Big) \ tilde {\ alpha} ^ \ theta. $$ In de laatste gelijkheid hebben we aangesloten op de golffunctie $ | n \ rangle = e ^ {\ mathrm {i} n \ theta} | \ mathrm {i} \ beta \ alpha ^ r (\ theta) = + 1 \ rangle $ gelabeld door het impulsmoment kwantumnummer $ n \ in \ mathbf {Z} $. De verschuiving $ 1/2 $ komt van de spin-verbinding (het fermion accumuleert de Berry-fase van $ \ pi $ terwijl $ \ mathrm {i} \ beta \ alpha ^ r $ om het gat slingert). Uit $ H_ \ phi $ kunnen we zien dat alleen $ \ pi $ -flux ($ \ phi = \ pi $) fermion nul-modi (bij $ n = 0 $) kan vangen in 2D gapped Dirac fermion-systemen.

Een monopooldefect (van de eenheidsterkte) in 3D kan worden beschouwd als het eindpunt van een $ 2 \ pi $ -fluxbuis. Stel dat de fluxbuis langs de $ x_3 $ -richting in een topologische isolator wordt geplaatst, waarbij de flux $ \ phi (x_3) $ verandert van $ 2 \ pi $ naar $ 0 $ over $ x_3 = 0 $. De effectieve Hamiltoniaan langs de buis is $$ H = \ mathrm {i} \ partiële_3 \ tilde {\ alpha} ^ 3 + m (x_3) \ tilde {\ alpha} ^ \ theta, $$ waarbij $ m (x_3) = n + \ frac {1} {2} - \ phi (x_3) / (2 \ pi) $ speelt de rol van een wisselende massa. $ \ tilde {\ alpha} ^ \ theta $ en $ \ tilde {\ alpha} ^ 3 $ zijn beperkingen van $ \ alpha ^ \ theta $ en $ \ alpha ^ 3 $ in de $ \ mathrm {i} \ beta \ alpha ^ r = + 1 $ subruimte.

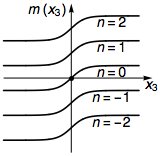
Alleen de impulsmoment $ n = 0 $ sector heeft een tekenverandering in de massa $ m (x_3) $, wat leidt tot de nulmodus gevangen door de monopool. De nulmodus wordt daarom gegeven door de projectie $ \ mathcal {P} = (1+ \ mathrm {i} \ beta \ alpha ^ r) (1+ \ mathrm {i} \ alpha ^ \ theta \ alpha ^ 3) / 4 $. Gebruikmakend van de bulkgrenscorrespondentie, als de monopool een nulmodus vastlegt in het grootste deel van een 3D TI, dan zal de oppervlakteafsluiting, die een $ 2 \ pi $ flux is, ook een nulmodus op het TI-oppervlak vangen. We concluderen dus dat de $ 2 \ pi $ -flux fermion nul-modi kan vangen in 2D gapless Dirac fermion-systemen.

Ik denk dat ik begrijp wat je bedoelt als je zegt dat je niet tevreden bent met het "niet-triviale bulktopologie-argument" als het gaat om het denken over edge-toestanden. Het Chern-getal (voor het onderbreken van tijdomkering) en $ \ mathbb {Z} _ {2} $ invariante (voor symmetrische tijdomkering) systemen, zoals DaniH suggereerde, geeft je inderdaad informatie over de randtoestanden; het Chern-getal en $ \ mathbb {Z} _ {2} $ invariant geven respectievelijk het aantal en de pariteit van edge-toestanden. Maar deze berekeningen zijn opnieuw afhankelijk van rechtstreeks omgaan met de niet-triviale bulktopologie. Het lijkt erop dat je meer geïnteresseerd bent in het expliciet zien van wat er aan de rand gebeurt. Er kunnen (mogelijk) veel manieren zijn om dit te doen; een zeer populaire waarvan ik op de hoogte ben, is de Jackiw-Rebbi -oplossing. Ik weet dat je een eenvoudig argument wilt zonder berekeningen; maak je geen zorgen, de onderstaande berekeningen zijn er alleen om uiteindelijk een punt te maken. Beschouw een 2D Dirac-model met een ruimtelijk variërende massa-term: $$ H = -iv_ {F} \ left (\ sigma_ {x} \ partiële_ {x} + \ sigma_ {y} \ partiële_ {y} \ right) + m (x) \ sigma_ {z} $$ waarbij $ \ lim_ {x \ rightarrow \ pm \ infty} m (x) = \ pm m_ {0} $ en het teken $ m (x) $ aan weerszijden van $ x = 0 $ blijft hetzelfde; in dat geval moeten we $ m (0) = 0 $ hebben. Als je de analogie van dit generieke Dirac-model met topologisch niet-triviale systemen beschouwt, zou je een topologisch niet-triviaal (triviaal) systeem hebben voor $ x<0 $ $ (x>0) $. Gebruikmakend van dezelfde randvoorwaarden die je beschreef, $ k_ {y} $ is nog steeds een goed kwantumgetal. Daarom kunnen we in de bovenstaande Hamiltoniaan $ i \ partiële_ {y} \ rightarrow k_ {y} $ vervangen; expliciet schrijven in matrixvorm krijgen we $$ H = \ left (\ begin {array} {cc} m (x) & -iv_ {F} (\ gedeeltelijke_ {x} -k_ {y}) \\ - iv_ {F } (\ Partial_ {x} + k_ {y}) & -m (x) \ end {array} \ right). $$ Je kunt oplossen voor de oplossingen $ \ Psi (x) = \ left (\ psi_ {1 } (x), \ psi_ {2} (x) \ right) ^ {T} \ equiv \ left (u (x), v (x) \ right) ^ {T} e ^ {ik_ {y} y} $ met energie $ E (k_ {y}) = v_ {F} k_ {y} $ als $$ \ left (\ begin {array} {cc} m (x) & -iv_ {F} (\ partiële_ {x} -k_ {y}) \\ - iv_ {F} (\ partiële_ {x} + k_ {y}) & -m (x) \ end { array} \ right) \ left (\ begin {array} {c} u (x) \\ v (x) \ end {array} \ right) = E \ left (\ begin {array} {c} u (x ) \\ v (x) \ end {array} \ right). $$ Als we naar de nulenergieoplossing kijken (door de meest geschikte $ k_ {y} = 0 $ te kiezen), krijgen we een set van eerste-orde gekoppelde differentiaalvergelijkingen $$ m (x) u (x) -iv_ {F} \ partiële_ {x} v (x) = 0 $$ en $$ - iv_ {F} \ partiële_ {x} u (x) -m (x) v (x) = 0 $$ De vergelijking voor $ v (x) $ na eliminatie is $$ \ partiële_ {x} ^ {2} v (x) = \ left (\ frac {m (x)} {v_ { F}} \ right) ^ {2} v (x) + \ frac {1} {m (x)} \ partieel_ {x} v (x) \ partieel_ {x} m (x). $$ De algemene oplossing zou $$ v (x) = C_ {1} \ sinh \ left (- \ frac {1} {v_ {F}} \ int dx \; m (x) \ right) + C_ {2} \ cosh \ zijn left (- \ frac {1} {v_ {F}} \ int dx \; m (x) \ right). $$ Implementeren van de fysiek relevante randvoorwaarden ($ \ lim_ {x \ rightarrow \ pm \ infty} v ( x) = 0 $) hebben we $$ v (x) \ propto \ exp \ left (- \ frac {1} {v_ {F}} \ int dx \; m (x) \ right). $$ Voor de eenvoudig (maar enigszins onfysisch) geval van $ m (x) = m_ {0} (2 \ theta (x) -1) $ het kan ve verklaard dat we een eenvoudige uitdrukking $$ v (x) \ propto \ exp \ left (- \ frac {m_ {0}} {v_ {F}} | x | \ right) krijgen. $$ toont de staat gelokaliseerd aan de rand. U kunt een meer fysieke uitdrukking krijgen voor $ v (x) $ (dwz een die vloeiend is op $ x = 0 $) door een $ m (x) $ te kiezen die minder abrupt verandert bij $ x = 0 $.

Ik realiseer me dat je op zoek bent naar een eenvoudig wiskundig argument om het bestaan ​​van randtoestanden te zien zonder het model op te lossen. Hoewel ik hierboven enkele triviale berekeningen heb uitgevoerd, is de conclusie dat wanneer een parameter (in dit geval $ m (x) $) in het model zijn kritische waarde (kritiek punt in het fasediagram) overschrijdt op een bepaald punt in de reële ruimte, je bent verwacht een randstatus te zien in de buurt van dat punt. Dit is op geen enkele manier een bewijs; Ik heb maar één voorbeeld gegeven!

Ik heb nog een laatste opmerking over " Ik denk dat er een reden moet zijn als de edge-modus robuust is. " Of de robuustheid van de edge-toestanden kan worden bepaald aan de hand van het model alleen hangt af van de complexiteit van het model. De robuustheid van de randtoestanden in topologische isolatoren is bijvoorbeeld het gevolg van tijdomkeringssymmetrie. Wanneer je de Hamiltoniaan opschrijft voor (bijvoorbeeld) de HgTe / CdTe-kwantumbron met behulp van het Bernevig-Hughes-Zhang (BHZ) -model als een $ 4 \ times4 $ -matrix (die ongeveer op het $ \ Gamma $ -punt geldt), construeer je je model zodanig dat het tijd-omkeringssymmetrie respecteert; het is niet andersom waar de robuustheid een gevolg is van het model. Bij het omgaan met het BHZ-model kan de robuustheid van randtoestanden worden beargumenteerd door de stelling van Kramer op de dispersie van de randtoestanden af ​​te dwingen. U kunt hierover meer lezen in: Welke conductantie wordt gemeten voor de kwantumspin Hall-toestand wanneer de Hall-conductantie verdwijnt?. Scrol helemaal naar beneden totdat je de vraag in het blokcitaat "" ziet. Ook: waarom is er slechts één schroeflijnvormige randtoestand per rand? Waarom moeten we er minstens één hebben en waarom kunnen we bijvoorbeeld niet twee staten per rand hebben? "

Waarom wil je inzicht hebben in de gapless edge states zonder bulktopologie te gebruiken? Als je me toestaat de bulktopologie te gebruiken, is een argument dat je continu de rand kunt verplaatsen en dat kunt beschouwen als een adiabatische parameter die twee systemen interpoleert. Om preciezer te zijn, kun je een bol beschouwen met een deel ervan in de ene topologische toestand A en de rest in een andere toestand B, zoals vacuüm. De interface tussen A en B is een cirkel. Als je nu begint bij B over de hele bol, en een klein eiland van A maakt, en dan A geleidelijk vergroot, beweegt de grenscirkel over de hele bol en krimpt hij weer tot nul. Je kunt de hele procedure zien als een interpolatie tussen B-fase en A-fase, en vanwege de bulktopologische invariant moet er tijdens een dergelijke procedure een opening zijn die de opening sluit, wat de reden is van randloze randtoestanden.